Operações com Ângulos
Adição,
Subtração, Multiplicação e Divisão de Ângulos.
Denominamos por ângulo a abertura formada por duas
semirretas que possuem a mesma origem.
A unidade usual de ângulo é o grau (representado
por º), por exemplo:
25º: lê-se vinte e cinco graus.
32º: lê-se trinta e dois graus.
120º: lê-se cento e vinte graus.
90º: lê-se noventa graus.
O grau possui dois submúltiplos: o minuto (representado por ’) e o segundo (representado por ”). Observe:
32’: lê-se trinta e dois minutos.
81’: lê-se oitenta e um minutos.
15”: lê-se quinze segundos.
45”: lê-se quarenta e cinco segundos.
Temos que 1º (um grau) corresponde a 60’ (sessenta minutos) e 1’ (um minuto) corresponde a 60” (sessenta segundos). Por exemplo, observe as transformações a seguir:
2º em minutos: 2 * 60 = 120’
12’ em segundos: 12 * 60 = 720”
3600’’ em minutos: 3600 : 60 = 60’
90000” em graus: 90000 : 60 = 1500’ e 1500 : 60 = 25º
Observação:
Tabela de conversões
25º: lê-se vinte e cinco graus.
32º: lê-se trinta e dois graus.
120º: lê-se cento e vinte graus.
90º: lê-se noventa graus.
O grau possui dois submúltiplos: o minuto (representado por ’) e o segundo (representado por ”). Observe:
32’: lê-se trinta e dois minutos.
81’: lê-se oitenta e um minutos.
15”: lê-se quinze segundos.
45”: lê-se quarenta e cinco segundos.
Temos que 1º (um grau) corresponde a 60’ (sessenta minutos) e 1’ (um minuto) corresponde a 60” (sessenta segundos). Por exemplo, observe as transformações a seguir:
2º em minutos: 2 * 60 = 120’
12’ em segundos: 12 * 60 = 720”
3600’’ em minutos: 3600 : 60 = 60’
90000” em graus: 90000 : 60 = 1500’ e 1500 : 60 = 25º
Observação:
Tabela de conversões
Adição
Dado os ângulos de 6º 25’ 36” e 4º 40’ 30”, a soma
entre eles é:
O resultado da soma é 10º 65’ 66”, porém podemos
apresentar o resultado de uma outra forma. Acompanhe a demonstração:
No ângulo de medida 10º 65’ 66”, temos que 65’ =
60’ + 5’ = 1º + 5’ e 66” = 60” + 6” = 1’ + 6”. Dessa forma, 10º 65’ 66” = 11º
6’ 6”.
Subtração
Dados os ângulos 54º 16’ 32” e 27º 18’ 40”, a
subtração entre eles é:
Observe que existem valores no minuendo que são
menores dos que os valores do subtraendo, quando isso acontece na subtração
temos que tirar do valor da esquerda completando o que está menor.
Ao retirarmos 1’ de 16’ ficaremos com 15’, sendo
que 1’ = 60” o qual deve ser somado a 32” resultando em 92”.
Agora devemos retirar 1º de 54º que será igual à
53º, considerando que 1º = 60’, temos 60’ + 15’ = 75’. Portanto:
O resultado da subtração é igual a 26º 57’
52”.
Transformações
de Ângulos
DE
GRAUS PARA MINUTOS E SEGUNDOS
Os ângulos são medidos em graus (1º) - e as subunidades dos
graus são os minutos (1º = 60') e os segundos (1' = 60"). Veja como fazer
a conversão entre essas unidades, tarefa que pode ser útil caso você necessite
fazer operações com medidas de ângulos.
Suponha que você tenha
que dividir um ângulo de 90° por 4:
Não é difícil veja:
O ideal, no entanto, é
que você apresente o resultado sem "vírgulas", mas transformando a
parte decimal (0,5) em minutos e segundos. Veja:
Para
transformar 0,5° em minutos vamos usar a regra de três simples:
Minutos e segundos
Em alguns casos, você
terá uma medida com minutos e segundos:
Transformando 0,12°:
Você tem, então,
minutos e "frações" de minutos.
Nova regra de três,
agora para passar minutos para segundos:
ADIÇÃO
11) Exemplo
17° 15´
10" + 30° 20´40"
17° 15´ 10"
30° 20´ 40"
-----------
47° 35´ 50"
12) Exemplo
13° 40´ +
30° 45´
13° 40´
30° 45´
--------
43° 85´ (simplificando) 44° 25´
SUBTRAÇÃO
Exemplo
58° 40´ -
17° 10´ =
58° 40´
17° 10´
-------
41° 30´
2) Exemplo
80° - 42° 30´ =
80°
42° 30´
-------
37° 30´
MULTIPLICAÇÃO DE
ÂNGULOS
Exemplo
17°15´ x 2 =
17°15´
x2
--------
34°30´
2°) Exemplo
24° 20´ x 3
=
24°20´
X 3
-------
72°60´ (simplificando) 73°
DIVISÃO DE UM ÂNGULO
POR UM NÚMERO
1º Exemplo
2º Exemplo
Ângulos
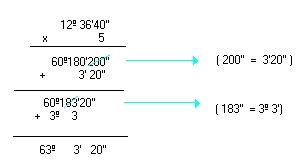
Multiplicação por um número natural
Observe os exemplos:
Divisão por um número natural
Observe os exemplos:
|
|||||||

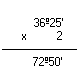
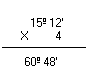
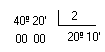
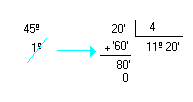
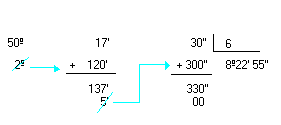
Muito bem explicado.
ResponderExcluirBem explicado
ResponderExcluirResolva as operações com angulos. A)39 52 15÷3
ResponderExcluirDivisão
ResponderExcluir19° 3'÷3
Falto mais exemplos da divisão
ResponderExcluirLá no tempo dos Sumérios não havia números natural, então como é dividir um ângulo por outro, exemplo: (30º 20') / (20º 5' 20")
ResponderExcluirOu multiplicar.
Excluir120 70' 20" 4. - 73 51' 34"/3 e quando e fracionado
ResponderExcluirExplicaçao top
ResponderExcluir120°6'50"+180°
ResponderExcluirOiiiuijjkk
ResponderExcluirDoido
Excluir